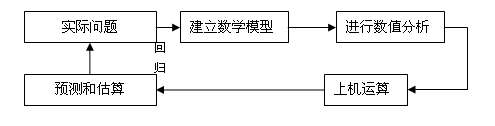
图1 数学建模思想
数学建模是对客观事物进行合理的抽象和量化，然后用公式模拟和验证的一种模式化思维。建立数学模型是处理数学科学理论问题的一个经典方法，也是处理各类问题的有效方法，是数学应用于科学和社会的最基本的途径。数学建模所研究的对象是日常生活和工程实践中的实际问题，把这些实际问题转化成数学问题过程就是数学建模的过程。所以数学建模和数学紧密相联，也就是说数学本身自始至终充满了数学模型。
三、应用数学模型

图2 应用模型过程
√了解问题的实际背景，明确其实际意义，掌握对象的各种信息。用数学语言来描述问题。
√根据实际对象的特征和建模的目的，对问题进行必要的简化，并用精确的语言提出一些恰当的假设。
√在假设的基础上，利用适当的数学工具来刻划各变量之间的数学关系，建立相应的数学结构（尽量用简单的数学工具）。
√利用获取的数据资料，对模型的所有参数做出计算（或近似计算）。
√对所得的结果进行数学上的分析。
√将模型分析结果与实际情形进行比较，以此来验证模型的准确性、合理性和适用性。如果模型与实际较吻合，则要对计算结果给出其实际含义，并进行解释。如果模型与实际吻合较差,则应该修改假设，再次重复建模过程。
√应用方式因问题的性质和建模的目的而异。
四、数学建模的作用
√培养学生的数学能力
数学建模的研究对象是一些实际问题，要把这些实际问题用数学语言表述出来并转化成抽象的数学问题并非易事。这就要求人们在建模过程中经过分析与综合、抽象与概括、比较与类比、系统化与具体化等阶段，这些阶段中能培养学生们的分析综合能力、抽象概括能力、想象洞察能力、运用数学工具的能力、通过实践验证数学模型的能力。
√激发学生学习数学的兴趣
数学建模改变了以教师为中心，只注重数学概念、定理的推理和证明，而忽视了数学知识的应用性的传统的数学教学模式，打造以学生为中心的全新的数学教学模式，培养学生的创造性，激发学生学习数学的兴趣。数学建模是抽象的数学知识和形象的实际问题的有力的结合，是数学知识得以应用的桥梁。
2003年（SARS的传播，露天矿生产的车辆安排），2004年（奥运会临时超市网点设计，电力输电阻塞管理），2005年（长江水质的评价和预测，DVD在线租赁）。
√培养学生知识的综合运用能力
在建立数学模型过程中，对于不同的实际问题，常常要用到不同的数学知识，如：高等数学、常微分方程、概率论与数理统计、运筹学、差分方程、组合数学、随即过程、计算方法、计算机模拟等等，在这就要求学生全面掌握并灵活运用这些数学知识。
√锻炼学生的动手能力
由于数学建模研究的是实际问题，传统的一根笔、一张纸已不能满足现实的需要，随着计算机的发展，各种数学软件包也随之产生，学生利用这些软件包把抽象的数学模型形象化、可视化，锻炼了学生的动手操作能力，激发了学生学习数学的兴趣。
√培养学生的自学能力
由于数学建模是对数学知识的综合应用，需要学生了解不同的数学类的知识，而高校普遍的数学课时都不能满足这种需求，这就需要教师挖掘学生的自学能力。教师在课堂上做引导，对数学知识做“串线式” 的讲解，让学生在课下对这些知识再做进一步的研究、探讨，以培养学生的自学能力。
√培养学生的创造性能力
由于数学建模的题目都来源于实际问题，解题的过程没有标准答案，这就需要教师鼓励学生提出自己的想法，大胆质疑，打破习惯的思维模式，利用自己已经学过的数学知识，展开联想，发挥个人的创造性，使问题得以解决。
五、总结
数学建模为学生架起了一座从数学知识到实际问题的桥梁。在数学建模过程中，学生不仅要有扎实的数学知识，能融会贯通，而且要求多接触实际，跨学科扩大知识面。数学建模为培养学生的多种能力提供了场所和途径，使学生的素质有了整体的提高，在高校数学教学改革中占有重要的地位。
希望此篇文章对我院学生重新认识高等数学在专业课学习和解决实际问题所起的重要作用和指导意义。